FP-growth 算法与Python实现

介绍
打开你的搜索引擎,输入一个单词或一部分,例如“我”,搜索引擎可能会去统计和“我”一块出现得多的词,然后返回给你。其实就是去找频繁项集,而且需要相当地高效,像Apriori那样的速度肯定是不行的了。
本文要介绍的是FP-growth算法,它被用于挖掘频繁项集,它把数据集存储为一个叫FP树的数据结构里,这样可以更高效地发现频繁项集或频繁项对。相比于Apriori对每个潜在的频繁项集都扫描数据集判定是否满足支持度,FP-growth算法只需要遍历两次数据库,因此它在大数据集上的速度显著优于Apriori。
本文的内容和代码主要来源于《机器学习实战》,加入一些自己的理解和测试,有兴趣可以去看看原书。
FP树
FP即Frequent Pattern,FP树看上去就是一棵前缀树,根节点是空集,结点上是单个元素,保存了它在数据集中的出现次数,出现次数越多的元素越接近根。此外,结点之间通过链接(link)相连,只有相似元素会被连起来,连起来的元素又可以看成链表。同一个元素可以在FP树中多次出现,根据位置不同,对应着不同的频繁项集。可以为FP树设置最小支持度,过滤掉出现次数太少的元素。
下面这个数据集构造FP树如下图所示。
| instance id | elements |
|---|---|
| 0 | r, z, h, j, p |
| 1 | z, y, x, w, v, u, t, s |
| 2 | z |
| 3 | r, x, n, o, s |
| 4 | y, r, x, z, q, t, p |
| 5 | y, z, x, e, q, s, t, m |
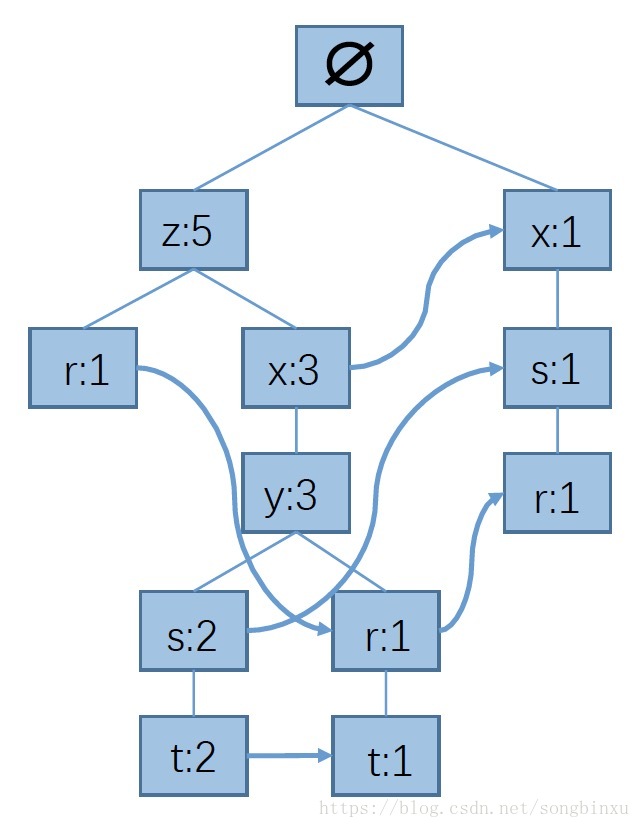
这棵树每个结点上都是一个单独的元素,及其在路径中的出现次数,例如"z:5"表示集合{z}出现了5次,而"x:3"表示集合{z,x}出现了3次,这是路径相关的。
FP树结点
树结点定义如下,name存放结点名字,count用于计数,nodeLink用于连接相似结点(即图中箭头),parent用于存放父节点,用于回溯,children存放儿子结点(即图中实线)。disp仅用于输出调试。
classtreeNode:def__init__(self, nameValue, numOccur, parentNode): self.name = nameValue self.count = numOccur self.nodeLink =None self.parent = parentNode self.children = {}definc(self, numOccur): self.count += numOccurdefdisp(self, ind=1):print' '*ind, self.name,' ', self.countfor childin self.children.values(): child.disp(ind+1)构建FP树
为了能方便地访问FP树种每一个不同的元素,需要为每种元素(的链表)设置一个头(header),这个header除了指向指定元素的第一个结点外,还可以保存该元素在数据集中的总出现次数。
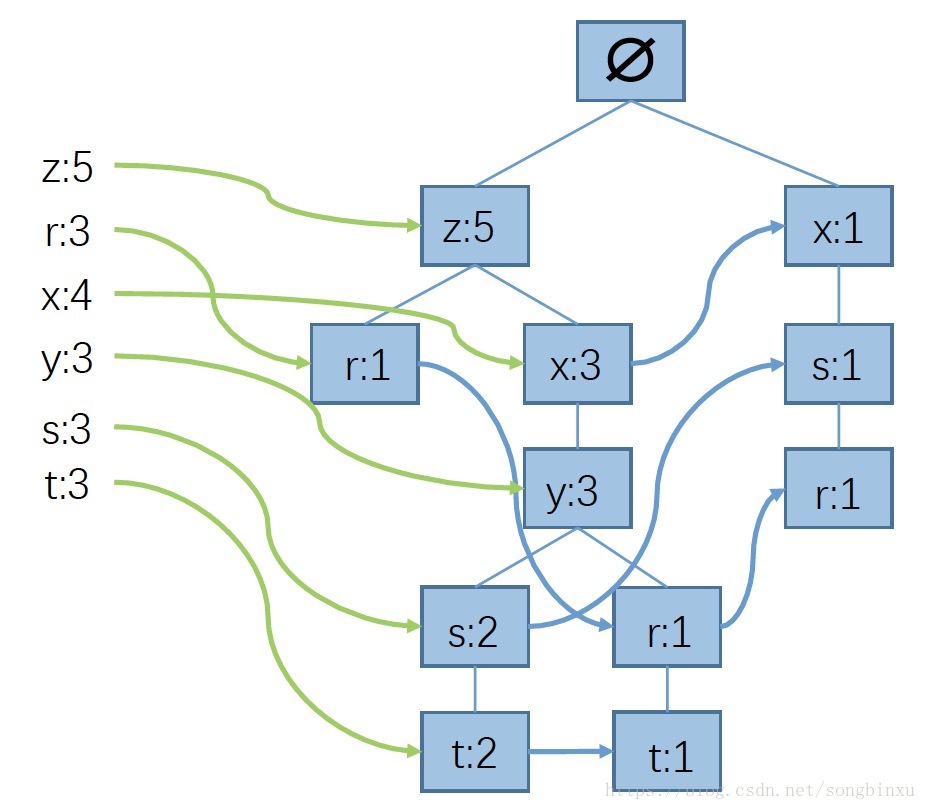
首先,遍历一次数据集,统计每个元素出现的次数,然后把出现次数较小的滤掉(例如选取最小支持度3,将出现次数小于3的元素滤除),然后对每个样本按照元素出现次数重排序。上面给出的数据集样例中,出现次数不小于3的元素有:z、r、x、y、s、t,滤除并重排后的样本如下所示。
| instance id | elements | filtered & sorted elements |
|---|---|---|
| 0 | r, z, h, j, p | r, z |
| 1 | z, y, x, w, v, u, t, s | z, x, y, s, t |
| 2 | z | z |
| 3 | r, x, n, o, s | x, s, r |
| 4 | y, r, x, z, q, t, p | z, x, y, r, t |
| 5 | y, z, x, e, q, s, t, m | z, x, y, s, t |
接着,构造FP树。从根节点∅开始,将过滤并排序后的样本一个个加入树中,若FP树不存在现有元素则添加分支,若存在则增加相应的值。下图给出了从根节点∅开始依次添加三个样本(过滤且排序)后FP的情况。
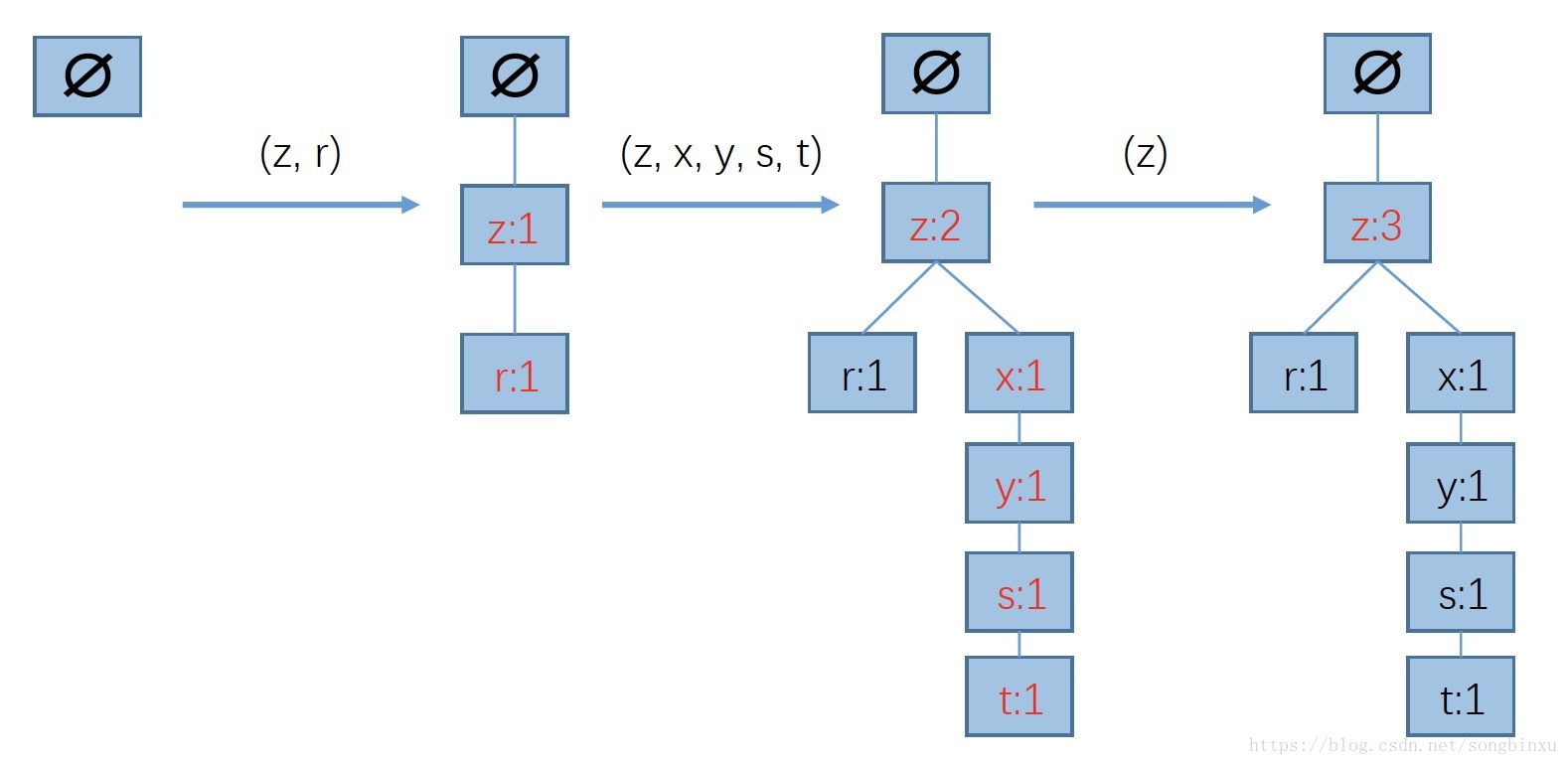
那么对于单个样本,FP树应该怎么生长呢?自然而然地想到递归。因为每个样本都是排序过的,频数高的频繁项集在前面,它总是更接近根结点,所以也可以把每个样本看成一棵子树,而我们要做的就是把子树添加到FP树里。因此每次只需判断第一个结点是否是根的儿子,若是则增加计数,若不是则增加分枝,然后递归调用构造FP树,传入第二个元素开始的子树即可。比如上例中往根节点∅增加样本(z,r)时,根没有z这个儿子,因此增加分支z。接着,只需递归地构造FP树,传入(r),发现当前FP树∅-z也没有r这个儿子,因此增加分支r。最终递归返回,引入样本(z,r)后构造的FP树就是∅-z-r。
下图详细地描述了这个过程,代码中updateFPtree()函数实现了这个功能。
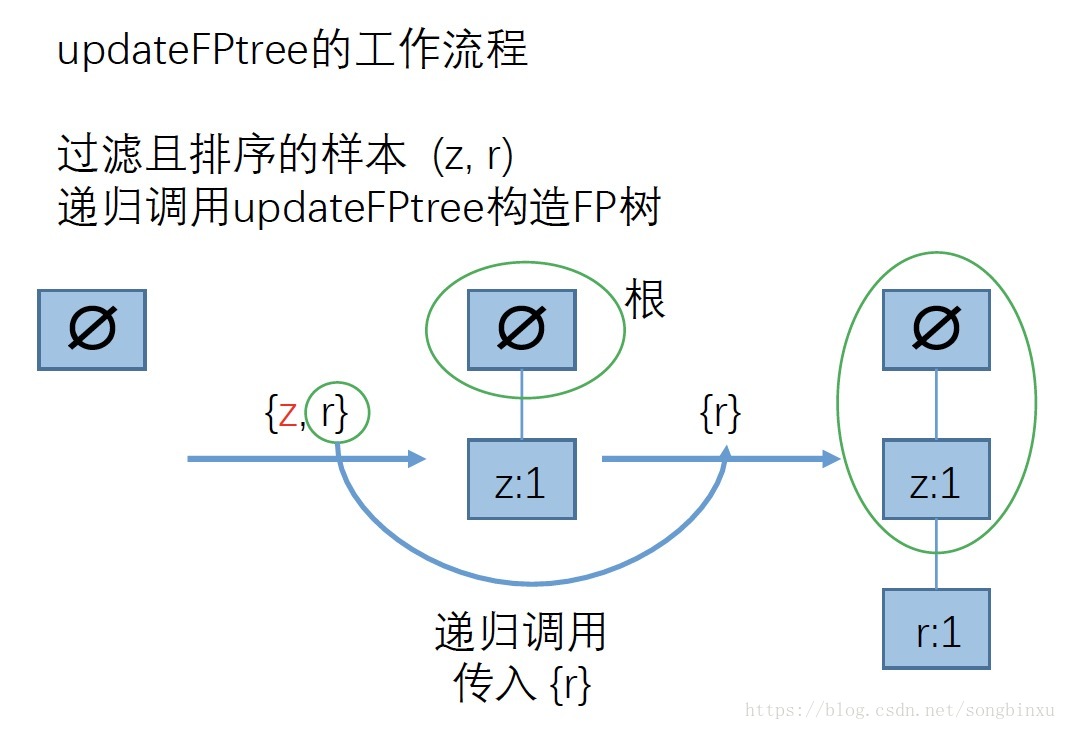
FP树构造代码实现
defupdateHeader(nodeToTest, targetNode):while nodeToTest.nodeLink !=None: nodeToTest = nodeToTest.nodeLink nodeToTest.nodeLink = targetNodedefupdateFPtree(items, inTree, headerTable, count):if items[0]in inTree.children:# 判断items的第一个结点是否已作为子结点 inTree.children[items[0]].inc(count)else:# 创建新的分支 inTree.children[items[0]] = treeNode(items[0], count, inTree)# 更新相应频繁项集的链表,往后添加if headerTable[items[0]][1] ==None: headerTable[items[0]][1] = inTree.children[items[0]]else: updateHeader(headerTable[items[0]][1], inTree.children[items[0]])# 递归if len(items) >1: updateFPtree(items[1::], inTree.children[items[0]], headerTable, count)defcreateFPtree(dataSet, minSup=1): headerTable = {}for transin dataSet:for itemin trans: headerTable[item] = headerTable.get(item,0) + dataSet[trans]for kin headerTable.keys():if headerTable[k] < minSup:del(headerTable[k])# 删除不满足最小支持度的元素 freqItemSet = set(headerTable.keys())# 满足最小支持度的频繁项集if len(freqItemSet) ==0:returnNone,Nonefor kin headerTable: headerTable[k] = [headerTable[k],None]# element: [count, node] retTree = treeNode('Null Set',1,None)for tranSet, countin dataSet.items():# dataSet:[element, count] localD = {}for itemin tranSet:if itemin freqItemSet:# 过滤,只取该样本中满足最小支持度的频繁项 localD[item] = headerTable[item][0]# element : countif len(localD) >0:# 根据全局频数从大到小对单样本排序 orderedItem = [v[0]for vin sorted(localD.items(), key=lambda p:p[1], reverse=True)]# 用过滤且排序后的样本更新树 updateFPtree(orderedItem, retTree, headerTable, count)return retTree, headerTable测试实例
# 数据集defloadSimpDat(): simDat = [['r','z','h','j','p'], ['z','y','x','w','v','u','t','s'], ['z'], ['r','x','n','o','s'], ['y','r','x','z','q','t','p'], ['y','z','x','e','q','s','t','m']]return simDat# 构造成 element : count 的形式defcreateInitSet(dataSet): retDict={}for transin dataSet: key = frozenset(trans)if retDict.has_key(key): retDict[frozenset(trans)] +=1else: retDict[frozenset(trans)] =1return retDict simDat = fpgrowth.loadSimpDat() initSet = fpgrowth.createInitSet(simDat) myFPtree, myHeaderTab = fpgrowth.createFPtree(initSet,3)# 最小支持度3 myFPtree.disp()输出结果如下,构造出来的FP树与上面给出的图是等价的。
Null Set1 x1 s1 r1 z5 x3 y3 s2 t2 r1 t1 r1从FP树挖掘频繁项集
从FP挖掘频繁项集的步骤如下:
- 从FP树提取条件模式基
- 用条件模式基构造FP树
- 重复1和2直到树只包含一个元素
提取条件模式基
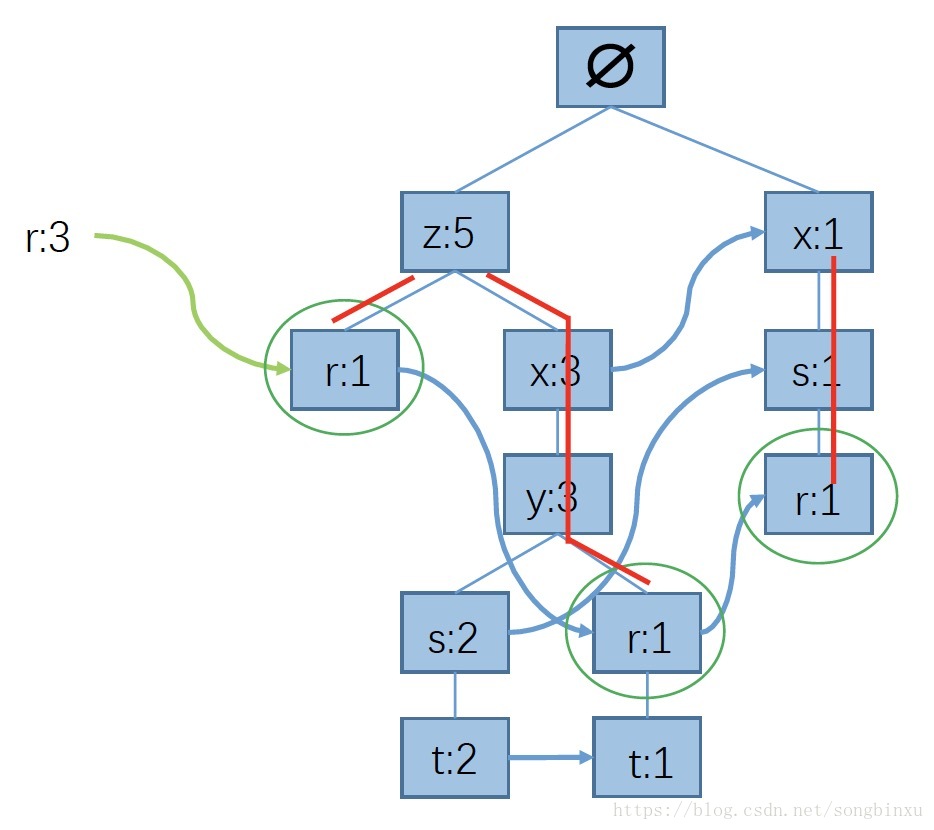
条件模式基(conditional pattern base)定义为以所查找元素为结尾的所有前缀路径(prefix path)的集合。我们要做的就是从header列表开始,针对每一个频繁项,都查找其对应的条件模式基。举个例子,如下图所示,元素"r"的前缀路径是{z}、{z,x,y}和{x,s}。同时,每一个路径要与起始元素的计数值关联。
| 频繁项 | 前缀路径集合(条件模式基) |
|---|---|
| z | {} 5 |
| r | {x,s} 1, {z,x,y} 1, {z} 1 |
| x | {z} 3, {} 1 |
| y | {z,x} 3 |
| s | {z,x,y} 2, {x} 1 |
| t | {z,x,y,s} 2, {z,x,y,r} 1 |
代码实现查找以目标元素结尾的所有路径(条件模式基)
# 递归回溯defascendFPtree(leafNode, prefixPath):if leafNode.parent !=None: prefixPath.append(leafNode.name) ascendFPtree(leafNode.parent, prefixPath)# 条件模式基deffindPrefixPath(basePat, myHeaderTab): treeNode = myHeaderTab[basePat][1]# basePat在FP树中的第一个结点 condPats = {}while treeNode !=None: prefixPath = [] ascendFPtree(treeNode, prefixPath)# prefixPath是倒过来的,从treeNode开始到根if len(prefixPath) >1: condPats[frozenset(prefixPath[1:])] = treeNode.count# 关联treeNode的计数 treeNode = treeNode.nodeLink# 下一个basePat结点return condPats测试用例
print fpgrowth.findPrefixPath('z', myHeaderTab)print fpgrowth.findPrefixPath('r', myHeaderTab)print fpgrowth.findPrefixPath('x', myHeaderTab)输出结果与上表是一致的,区别在于省略了空集。
{} {frozenset(['x','s']):1, frozenset(['z']):1, frozenset(['y','x','z']):1} {frozenset(['z']):3}创建条件FP树
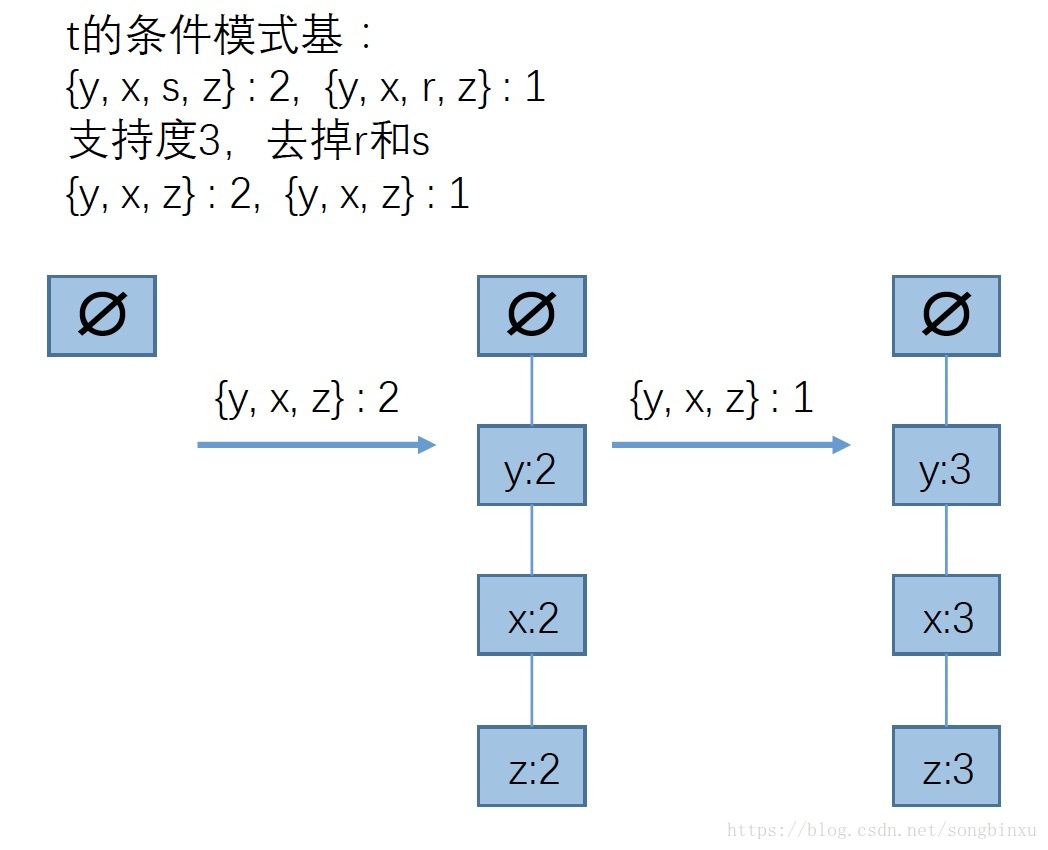
对每一个频繁项,都建立一棵条件FP树。上面我们对每一个频繁项提取了条件模式基,现在就用它作为输入数据,即把每一个前缀路径当成一个样本,调用createFPtree()构造一棵FP树,即条件FP树。然后,对这个条件FP树,递归地挖掘。由于createFPtree()中含有过滤的功能,因此最终总能获得所有满足最小支持度的频繁项,即我们所需要的频繁项集。
defmineFPtree(inTree, headerTable, minSup, preFix, freqItemList):# 最开始的频繁项集是headerTable中的各元素 bigL = [v[0]for vin sorted(headerTable.items(), key=lambda p:p[1])]# 根据频繁项的总频次排序for basePatin bigL:# 对每个频繁项 newFreqSet = preFix.copy() newFreqSet.add(basePat) freqItemList.append(newFreqSet) condPattBases = findPrefixPath(basePat, headerTable)# 当前频繁项集的条件模式基 myCondTree, myHead = createFPtree(condPattBases, minSup)# 构造当前频繁项的条件FP树if myHead !=None:# print 'conditional tree for: ', newFreqSet# myCondTree.disp(1) mineFPtree(myCondTree, myHead, minSup, newFreqSet, freqItemList)# 递归挖掘条件FP树测试
获取数据集中出现次数不小于3的组合。
simDat = fpgrowth.loadSimpDat() initSet = fpgrowth.createInitSet(simDat) myFPtree, myHeaderTab = fpgrowth.createFPtree(initSet,3) freqItems = [] fpgrowth.mineFPtree(myFPtree, myHeaderTab,3, set([]), freqItems)for xin freqItems:print x输出结果,可以对照一下,这些组合出现的次数都至少为3。
set(['y']) set(['y','x']) set(['y','z']) set(['y','x','z']) set(['s']) set(['x','s']) set(['t']) set(['y','t']) set(['x','t']) set(['y','x','t']) set(['z','t']) set(['x','z','t']) set(['y','x','z','t']) set(['y','z','t']) set(['r']) set(['x']) set(['x','z']) set(['z'])代码中存在的bug
出于测试,我把createFPtree中的最小支持度改成了2,意思是允许出现次数为2的单元素频繁项p和q参与进来,理论上mineFPtree生成的频繁项集应当只增无减才对,然而结果却是减少了,而且频繁项{y,x,z,t}不见了,说明代码有问题。
经过排查,我认为错误出在按照频次对样本过滤与排序那里。如果有两个元素频次相同,python2的稳定排序会保持他们在原本字典中的顺序。为了解决这个问题,需要修改createFPtree函数中对样本排序的部分,使得两元素在频次相同时按照字母顺序排序。
defcreateFPtree(dataSet, minSup=1): ...if len(localD) >0:# 根据全局频数从大到小对单样本排序 orderedItem = [v[0]for vin sorted(localD.iteritems(), key=lambda p:(p[1], -ord(p[0])), reverse=True)]示例: 从新闻网站点击流中挖掘
数据集kosarak.dat可以从这里下载,它的每一条记录是某个用户浏览过的新闻报道,总共99w条样本,新闻报道被编码成index。使用FP-growth,查看有哪些新闻报道集合被超过10w人浏览。
# 准备数据with open("./data/kosarak.dat","rb")as f: parsedDat = [line.split()for linein f.readlines()] initSet = fpgrowth.createInitSet(parsedDat)# 用数据集构造FP树,最小支持度10w myFPtree, myHeaderTab = fpgrowth.createFPtree(initSet,100000)# 挖掘FP树 freqItems = [] fpgrowth.mineFPtree(myFPtree, myHeaderTab,100000, set([]), freqItems)for xin freqItems:print x输出结果如下,在我的macbook上,整个过程仅耗时13秒。
set(['1']) set(['1','6']) set(['11']) set(['11','3']) set(['11','3','6']) set(['11','6']) set(['3']) set(['3','6']) set(['6'])针对上面提到的bug,由于kosarak.dat中的元素都是字符串化的整数,故createFPtree中排序的部分应该修改成:
... orderedItem = [v[0]for vin sorted(localD.iteritems(), key=lambda p:(p[1], int(p[0])), reverse=True)]总结
FP-growth其实是一种特殊的数据结构的应用,本质上是某种前缀树+相似元素链表的结构。FP-growth算法提供了一种相对更快的发现频繁项集的方法,它之所以快,是因为它只遍历1次数据集,即可将整个数据集构造成一棵FP树,之后从FP树中发现频繁项集。提取出频繁项集之后,就可以进一步挖掘关联规则,比如Apriori算法中的方法(详情可见这里)。
书中算法的实现大量使用了递归,这里可能有个问题,就是递归层数过深。
完整代码
https://github.com/SongDark/FPgrowth
参考资料
《机器学习实战》
FP-growth算法高效发现频繁项集(Python代码)